Тернарный поиск
Содержание
Тернарный поиск
Описание алгоритма
Научимся искать локальный максимум некоторой непрерывной функции $f$ на отрезке $[l, r]$. Будем считать, что на данном отрезке есть только один локальный максимум, то есть $f$ сначала возрастает, а потом убывает.
Будем подерживать следующий инвариант - икомый максимум лежит на отрезке $[l, r]$. Границы будем постепенно сдвигать к искомой точке, почти как в бинарном поиске.
Поделим текущий отрезок на три равные части. Получим отрезки: $\left[l, m_1\right]$, $[m_1, m_2]$, $[m_2, r]$. Теперь сравним значения в точках $m_1$ и $m_2$.
- Если $f(m_1) > f(m_2)$, то максимум функции лежит на $[l, m_2]$. Правее $m_2$ его быть не может, так как тогда на $[m_1, m_2]$ функция убывает, а потом на $[m_2, m_3]$ возрастает, но мы требуем, чтобы сначала шел спад, а потом рост. Сдвинем границы следующим образом: $r \rightarrow m_2$.
- Если $f(m_1) < f(m_2)$, то максимум лежит на $[m_1, r]$ по тем же соображениям, что и в предыдущем пункте. Изменим границы: $l \rightarrow m_1$.
Асимптотика
Заметим, что длина каждого отрезка разбиения составляет одну треть от исходного, то есть длина отрезка, на котором мы ищем максимум каждый раз умножается на $\frac{2}{3}$. Если мы делаем поиск на массиве из $n$ элементов, то мы сделаем примерно $\log_{3/2}n$ итераций. То есть асимптотика составит $O(\log n)$, так как мы игнорируем основание логарифма.
Альтернативное решение
Как известно, локальный максимум функции $f$ - это просто такое $x_0$, что для всех близких к нему $x$ значения $f(x) < f(x_0)$. Для непрерывных функций выполняется более сильное условие: слева от максимума функция возрастает, а справа от максимума функция убывает. Воспользуемся этим условием в бинарном поиске.
Если известно $x_1$ такое, что в его окрестности f(x) возрастает, и $x_2$ такое, что в его окрестности f(x) убывает, то можно запустить между ними бинпоиск и найти точку $x_0$ такую, что слева от нее возрастает значение функции, а справа - убывает. Это и есть локальный максимум.
А если функция выпуклая, то она вообще выглядит красиво: сначала возрастает, потом максимум, потом убывает.
Чтобы по точке понять, значение функции убывает или возрастает в ее окрестности , достаточно проверить две точки достаточно близко к ней и сравнить значения $f$ в этих точках.
Примечание: такой подход еще называют бинарным поиском по производной, так как сначала производная больше нуля, а потом меньше нуля.
Отрезки с постоянным значением
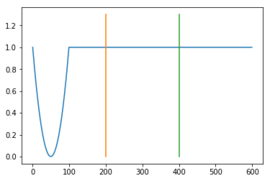
В описании функции $f$ мы потребовали строгое возрастание и убывание. Объясним это ограничение. Для этого предположим, что возможна нестрогая монотонность.
Будем искать локальный минимум. Допустим, у функции есть отрезок, где ее значение постоянно. Отрезок поиска может измениться здесь двумя способами - в зависимости от того, в какую из частей поиск идет при равенстве. Если левая граница сдвинется на оранжевую линию, то поиск останется на отрезке со значением $1$, что гораздо больше, чем настоящий локальный минимум $0$.
Автор конспекта: Полина Романченко
По всем вопросам пишите в telegram @Romanchenko