Дерево доминаторов
Наверное это самый худший конспект, который есть на этом сайте. Даже автор через год после написания на смог его понять. Но так как всё равно никаких других конспектов по дереву доминаторов нет (потому что это нахрен никому не нужный алгоритм), то пусть этот конспект тут останется и будет отпугивать людей.
Содержание
Определение
Представим себе ориентированный граф, в котором есть какая-то начальная вершина $S$, из которой все остальные достижимы. В таком графе вершина $A$ доминирует над вершиной $B$, если любой путь из $S$ в $B$ проходит через $A$. В частности, вершина $S$ доминирует над всеми вершинами.
Заметим, что из определения следует, что если посмотреть на любой путь из $S$ в $B$, то все доминаторы $B$ будут лежать на этом пути. Вершина $A$ называется непосредственным доминатором вершины $B$, если не существует вершины $C$, такой что $C$ доминатор $B$ и $C$ лежит на пути из $A$ в $B$. Другими словами непосредственный доминатор это самый ближайших доминатор к вершине. Далее непосредственный доминатор обозначается за $idom(B)$.
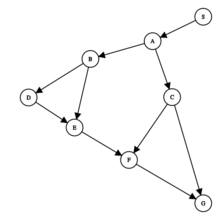
Рассмотрим пример справа. У всех вершин кроме $S$ есть хотя-бы один доминатор — вершина $S$. Так же вершина $A$ является доминатором для всех вершин кроме $A$ и $S$. Так же вершина $B$ является доминатором для $D$ и $E$. При этом $idom(A) = S$, $idom(B) = A$, $idom(C) = A$, $idom(D) = B$, $idom(E) = B$, $idom(F) = A$, $idom(G) = A$.
Заметим, что доминаторы образуют структуру дерева, т.е. если $A$ — доминатор $B$ и $B$ — доминатор $C$, то $A$ — доминатор $C$. И тогда всех доминаторов можно представить в виде дерева, где непосредственным предком вершины является её $idom$.
Алгоритм
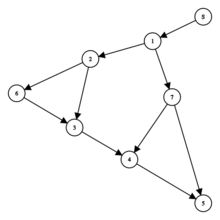
Возьмём наш ориентированный граф и запустимся DFSом. Теперь перенумеруем вершины в порядке входа DFSа в эти вершины. В показанном ранее графе теперь вершины будут иметь номера как на рисунке справа. Так как все доминаторы лежат на любом пути из $S$ в $A$, то можно заметить, что доминаторы $A$ будут так же лежать на пути из $S$ в $A$ в дереве обхода DFS и соответственно будут иметь меньшие номера, чем $A$.
Полудоминаторы
Определение
Мы уже пронумеровали вершины в порядке обзода DFS. Теперь можно ввести понятие полудоминатор. Полудоминатором вершины $A$ называется вершина с минимальным номером, такая что из неё есть путь в $A$ по вершинам, номер которых строго больше номера $A$. Далее обозначается за $sdom(A)$.
Заметим, что предок в дереве обхода DFS имеет меньший номер, чем сама вершина, так что у любой вершины есть её полудоминатор. В примере справа $sdom(1) = S$, $sdom(2) = 1$, $sdom(3) = 2$, $sdom(4) = 1$, $sdom(5) = 1$, $sdom(6) = 2$, $sdom(7) = 1$.
Кстати говоря полудоминатор зависит от обхода dfs, и при разных обходах могут быть разные нумерования вершин и разные полудоминаторы.
Свойства полудоминаторов
Заметим, что $sdom(A)$ обязательно должен лежать на пути из корня в $A$ в дереве обхода DFS. Это верно, т.к. номер $sdom(A)$ меньше номера $A$, а значит $DFS$ сначала зашёл в $sdom(A)$, а потом должен был зайти в $A$. Но т.к. есть путь от $sdom(A)$ в $A$, то значит DFS до выхода из $sdom(A)$ должен был ранее обойти все ранее не посещённые достижимые от него вершины, а значит должен был зайти и в $A$, т.е. $A$ в поддереве $sdom(A)$ в дереве DFS.
Может показаться, что $sdom(A)$ равен $idom(A)$. Но вообще-то говоря это не обязательно верно. Однако мы знаем, что и $idom(A)$ и $sdom(A)$ лежат на пути из $S$ в $A$ в дереве обхода $DFS$. Тогда заметим, что $idom(A)$ должен лежать на пути из $S$ в $sdom(A)$. (Т.е сначала идёт непосредственный доминатор, а уже потом идёт полудоминатор) Это верно т.к. в противном случае любой путь из $sdom(A)$ в $A$ проходит через $idom(A)$, а значит по определению полудоминатора номер $idom(A)$ будет больше номера $A$. Но $idom(A)$ лежит на пути в дереве DFS из $S$ в $A$, а значит номер $idom(A)$ должен быть меньше номера $A$. Противоречие. Значит утверждение доказано.
Нахождение полудоминаторов
Раз мы определили этот странный полудоминатор, наверное он нам потом понадобится и нам придётся как-то найти его. Заметим следующий факт. Пусть есть вершина $A$. Тогда её полудоминатором может являться какая-то из вершин, от которой непосредственно ведёт ребро к $A$. Если же никакая такая вершина не является полудоминатором вершины $A$, то возьмём любую вершину $B$, из которой ведёт ребро в $A$ и котора по номеру больше $A$. Теперь возьмём все вершины на пути от $S$ к $B$ в дереве обхода DFS, у которых номер больше, чем у $A$. (Другими словами мы смотрим, когда путь от $S$ к $B$ ответвился от пути от $S$ к $A$, и дальше смотрим на все вершины на этом ответвлении). Утверждается, что полудоминатор $A$ это минимальный по номеру среди всех полудоминаторов вершин на этих ответвлениях для всех возможных $B$.
Докажем это возьмём $C$ — полудоминатор $A$. Если он связан напрямую ребром с $A$, то мы победили. Иначе у нас есть пути из $C$ в $A$ по вершинам, большим чем $A$ и заметим, что последняя вершина на пути из $C$ в $A$ имеет номер больший, чем $A$ и из неё есть ребро в $A$, т.е. это как раз определяемая ранее вершина $B$. Теперь на этом же пути из $C$ в $A$ найдём минимальную по номеру вершину. Это какая-то вершина $D$. Заметим, что $C$ подходит под определение полудоминатора для $D$ (т.к. все остальные вершины на пути имеют больший номер, чем $D$), а значит полудоминатор $D$ это $C$ или какая-то меньшая по номеру вершина. Однако заметим, что полудоминатор $D$ обязательно является полудоминатором $A$, т.к. из него есть путь по вершинам, номер которых больше номера $D$, а соответственно больше номера $A$, а так же из $D$ есть путь по вершинам, номер которых больше $A$. Тогда полудоминатор $D$ это $C$. Осталось только показать, что $D$ лежит на пути из $S$ в $B$. Т.к. $D$ имеет меньший номер, чем $B$, то DFS сначала зашёл в $D$, а уже потом в $B$. И т.к. $B$ достижима из $D$, то значит из $D$ есть путь до $B$ в дереве обхода DFS.
Алгоритм поиска полудоминаторов
Будем пользоваться предыдущим наблюдением. Переберём вершины в обратном порядке к тому, в котором мы их перебирали в DFS. Алгоритм за $N^2$ довольно тривиальный. Рассмотрим вершину $A$, переберём все те вершины, из которых в неё идут рёбра. Если такая вершина $B$ меньше по номеру, то она кандидат на доминатор. Иначе же кандидаты на доминатор — доминаторы всех уже рассмотренных вершин, которые лежат в дереве обхода DFS на пути в $B$. При этом все такие вершины на самом деле представляют собой последовательный путь в этом дереве, начиная с какой-то вершины и заканчивая в $B$. При этом в дальнейшем когда мы будем рассматривать следующие вершины, то этот путь будет полностью вкладываться в некоторые другие пути. Поэтому по аналогии с СНМ замутим тут сжатие путей. При этом когда мы сжимаем путь мы будем сразу запоминать минимальный доминатор по пожатой части. Возможно потом я подробнее тут напишу, что я хочу, но надеюсь и так понятно. (нихрена не понятно)
Поиск доминаторов
Несколько замечаний
Заметим такую вещь: если есть вершины $A$ и $B$, такие что $B$ лежит на пути из $idom(A)$ в $A$ в дереве обхода DFS, то $idom(B)$ должен лежать на пути от $idom(A)$ в $B$ в дереве обхода DFS. Другими словами доминаторы вложены друг в друга. Это верно так как любой путь из $S$ в $B$ можно продлить до $A$, а значит они все проходят через $idom(A)$, значит $idom(B)$ на может быть больше $idom(A)$.
Теперь заметим, что если есть вершина $A$ и есть $B$ — $sdom(A)$. Заметим, что если $B$ не является $idom(A)$, то мы уже знаем, что $idom(A)$ идёт раньше в дереве обхода DFS чем $sdom(A)$. И т.к. они не равны, то есть путь от $idom(A)$ в $A$, не проходящий через $sdom(A)$. Тогда возьмём такой путь. Он сначала идёт по дереву обзода DFS, дальше ответвляется и потом приходит в какую-то вершину $C$ на пути от $sdom(A)$ до $A$. Тогда заметим, что ответвление должно проходить полностью по вершинам, по номеру большим, чем $C$. Тогда $sdom(C)$ по номеру меньше $sdom(A)$. Теперь посмотрим на все вершины на пути от $sdom(A)$ в $A$ по дереву обхода DFS. Утверждается, что $idom(A)$ равен минимуму по $idom$ от всех вершин на пути. Пусть это не так. Заметим, что $idom(A)$ точно не больше чем $idom$ от всех вершин на пути от $sdom(A)$ к $A$ (из утверждения выше). Тогда пусть $idom(A)$ меньше чем $idom$ всех этих вершин. Тогда есть путь от $idom(A)$ к $A$, не проходящий ни через один другой $idom$. Этот путь идёт по каким-то вершинам на пути из $S$ к $A$ в дереве DFS, иногда отстыковывается от него. Посмотрим на тот момент времени, когда он отстыковался от него на вершине, которая была на пути из $S$ в $sdom(A)$ до $sdom(A)$, а пристыковался на вершине на пути из $sdom(A)$ в $A$. Если он не пристыковался к $A$, то у той вершины, к которой он пристыковался есть путь от $S$ к ней, не проходящий через её $idom$, что невозможно. Иначе этот путь пристыковывается к $A$, а т.к. он отстыкованный, то в нём номера всех вершин больше $A$. При этом он отстыковался раньше $sdom(A)$. Значит $sdom(A)$ не является минимальным. Противоречие. Значит такого нет. (На самом деле тут есть лажа, но мне вломас править)
Теперь пусть $sdom(A)$ является $idom(A)$. Тогда, что у любой вершины на пути из $sdom(A)$ в $A$ в дереве обхода DFS её $idom$ тоже лежит на этом пути (было ранее показано), а значит и $sdom$ от любой вершины на пути тоже больше чем $sdom(A)$. При этом мы уже поняли, что если $sdom(A)$ не $idom(A)$, то есть вершина на пути от $sdom(A)$ в $A$, у которой $sdom$ меньше $sdom(A)$. Значит если у любой вершины $sdom$ от неё меньше чем $sdom$ от $A$, то $sdom(A)$ это $idom(A)$.
Алгоритм
В принципе мы уже знаем как искать $idom(A)$. Нам достаточно перебрать все вершины на пути из $sdom(A)$ в $A$ в дереве обхода $DFS$. Если этот путь состоит из 1 ребра, то так как там вообще нет вершин, то нет и вершин, у которых $sdom$ меньше $sdom(A)$. Значит $sdom(A)$ это и есть $idom(A)$. Иначе же там есть всякие вершины, при этом если есть вершина, у которой $sdom$ меньше $sdom(A)$, то мы ищем минимальный $idom$ у всех вершин на пути дерева обхода DFS от $sdom(A)$ в $A$. Если у всех вершин их $sdom$ больше $sdom(A)$, то $sdom(A)$ это $idom(A)$, при этом если посмотреть на первую вершину на пути из $sdom(A)$ в $A$, то её $sdom$ не меньше её предка, который является $sdom(A)$. Так же её $sdom$ не меньше её $idom$, что не меньше $idom(A)$, что равно $sdom(A)$. Короче говоря тогда получим, что тоже максимальный $idom$ на пути от $sdom(A)$ к $A$ это $idom(A)$. Тогда у нас есть следующая задача: для вершины в дереве узнать минимум на отрезке от какого-то её предка до неё и присвоить себе это значение. Это можно решать миллиардом способов, например ДО, двоичными подъёмами или стеком.
Автор конспекта: Филипп Грибов
По всем вопросам пишите в telegram @grphil
Вообще я с самого начал не хотел это писать, но у меня чутка пригорело что нигде нормально про это не написанно. Тут конечно тоже нихрена не понятно, но видит бог, я пытался.