Суффиксный автомат: различия между версиями
Grphil (обсуждение | вклад) |
Grphil (обсуждение | вклад) |
||
| Строка 14: | Строка 14: | ||
Автомат называется '''детерминированным''', если из любого состояния не существует двух переходов по одинаковым символам. Это означает, что для каждой строки есть не более одного пути, соответствующего ей и передав строку автомату мы однозначно знаем, куда по ней мы перейдём, если путь по ней существует. | Автомат называется '''детерминированным''', если из любого состояния не существует двух переходов по одинаковым символам. Это означает, что для каждой строки есть не более одного пути, соответствующего ей и передав строку автомату мы однозначно знаем, куда по ней мы перейдём, если путь по ней существует. | ||
| − | Автомат называется '''конечным''', если | + | Автомат называется '''конечным''', если нём конечное число вершин. |
Некоторые вершины автомата будут помечены как '''терминальные'''. Считается, что '''автомат принял строку''' если существует путь, соответствующий этой строке и в конце, пройдя по пути, мы окажемся в терминальной вершине. | Некоторые вершины автомата будут помечены как '''терминальные'''. Считается, что '''автомат принял строку''' если существует путь, соответствующий этой строке и в конце, пройдя по пути, мы окажемся в терминальной вершине. | ||
Текущая версия на 17:18, 11 марта 2020
Содержание
Автомат
Здесь суффиксный автомат описан совсем не так, как это принято, зато это гораздо понятнее.
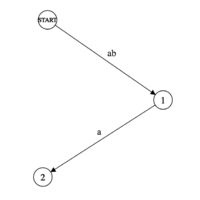
Представим себе ориентированный граф, в котором на каждом ребре записано по букве. Так же выделим одну из вершин и назовём её стартовой. Замечаем, что в таком графе каждый путь от стратовой вершины до какой-то будет задан определённой строкой. Рассмотрим следующий пример:
В автомате 3 вершины: start, 1, 2, есть ребро от start к 1, на котором написаны буквы «a» и «b» и есть ребро от 1 к 2, на котором написано «c». Заметим, что в таком автомате от start есть 5 путей: пустой путь, путь через «a» в 1, путь через «b» в 1, путь через «a» а потом через «c» в 2, пусть через «a» а потом через «c» в 3. Т.е возможные пути заданы строками «», «a», «b», «ac», «bc».
Таким образом в автомат можно передать строки и итерируясь по символам строки можно переходить из одной вершины в другую. В предыдущем примере в автомат можно передать строку «ac» и после этого мы окажемся в вершине 2. Но строку «bd» в предыдущий автомат передать нельзя, так как из 1 нет ребер по символу «d».
Основные понятия
В автомате вершины принято называть состояниями, а рёбра — переходами.
Автомат называется детерминированным, если из любого состояния не существует двух переходов по одинаковым символам. Это означает, что для каждой строки есть не более одного пути, соответствующего ей и передав строку автомату мы однозначно знаем, куда по ней мы перейдём, если путь по ней существует.
Автомат называется конечным, если нём конечное число вершин.
Некоторые вершины автомата будут помечены как терминальные. Считается, что автомат принял строку если существует путь, соответствующий этой строке и в конце, пройдя по пути, мы окажемся в терминальной вершине.
Суффиксный автомат
Определение:
Суффиксный автомат —это конечный детерминированный автомат, принимающий все суффиксы данной строки и только их.
Если это определение у вас вызвало ужас и абсолютное непонимание происходящего, посмотрите все термины в предыдущем разделе. Далее все эти страшные слова мы почти не будем использовать.
| Примеры автоматов | ||
|---|---|---|
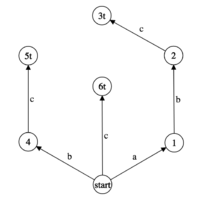
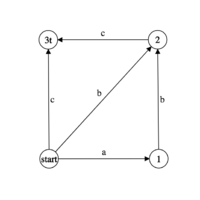
| Бор, построенный на всех суффиксах строки нам вполне подойдёт. Для примера возьмём строку «abc» | Для той же строки можно построить суффиксный автомат гораздо меньшего размера: | Для строки «aabab» можно обойтись всего 7 вершинами. Запомните эту строку, её удобно использовать для дебага. |
А теперь перейдём к алгоритму, строющему суффиксный автомат размера $O(n)$, где $n$ — длина строки. Теория будет сильно отличаться от общепринятой в сторону большей понятности. Но для начала введём некоторые дополнительные правила и заметим некоторые вещи.
Дополнительные правила
Для каждой вершины в автомате есть какой-то набор строк, пути по которым заканчиваются в этой вершине. Тогда будем поддерживать следующее правило. Для каждой вершины все строки, ведущие в неё должны являться суффиксами друг друга. Причём эти суффиксы должны являться подряд идущими по длине. Т.е если $s$ — максимальная по длине строка, которая ведёт в вершину и если $k$ — длина $s$, то в вершину ведут строки $s[0:k], s[1:k], s[2:k], s[3:k], \ldots, s[l:k]$. Итого в вершину будет вести $l + 1$ строка, причём все строки будут является суффиксами $s$ длины хотя-бы $k - l$. Соответственно наборы («z») или («abc», «bc», «c») или («abacaba», «bacaba», «acaba») могут являться полным набором строк, ведущих в вершину, а наборы («abacaba», «abacab») или («abcd», «cd», «d») или («abacab», «bacab») не могут являться полным набором строк, ведущих в вершину.
Будем говорить, что вершине соответствует максимальная строка, которая в неё ведёт. Т.е. если в вершину ведёт единственная строка («z»), то этой вершине соответствует «z», если в вершину ведут строки («abc», «bc», «c»), то вершине соответствует «abc», если в вершину ведут строки («abacaba», «bacaba», «acaba»), то вершине соответствует строка «abacaba».
По аналогии с Ахо-Карасиком, мы можем ввести понятие суффиксная ссылка. Как мы уже знаем, вершина $A$ принимает строки $s[0:k], s[1:k], s[2:k], s[3:k], \ldots, s[l:k]$ (Суффиксы $s$ длиной $k, k - 1, \ldots, k - l$). А где-то должна быть вершина $B$, в которую ведёт строка $s[l + 1:k]$ (Суффикс $s$, имеющий длину $k - l - 1$). Ещё одним правилом суфф. автомата будет то, что максимальная по длине строка, которая ведёт в $B$ должна быть $s[l + 1:k]$. И тогда все строки, которые ведут в $B$ будут иметь вид $s[l + 1:k], s[l + 2:k], \ldots, s[l + t:k]$, (суффиксы $s$, имеющие длину от $k - l - t$ до $k - l - 1$). Другими словами вершина $B$ будет принимать следующие суффиксы $s$ после вершины $A$. Тогда будем считать, что из $A$ суффиксная ссылка ведёт в вершину $B$. Тогда из каждой вершины кроме стартовой будет по одной суффиксной ссылке.
Важные замечания
Тогда заметим несколько важных вещей. Возьмём любую вершину $A$. Заметим, что так как все строки, которые в неё ведут, являются суффиксами друг друга, то они все заканчиваются на один и тот же символ. Значит все переходы в $A$ ведутся по одному и тому же символу, и только по нему.
Вообще в $A$ могут вести переходы из разных вершин. Каждой из них соответствует какая-то строка. Ту из них, которой соответствует самая длинная строка, будем называть предком вершины $A$.
Как мы уже знаем, в вершину $A$ ведут строки $s[0:k], s[1:k], s[2:k], s[3:k], \ldots, s[l:k]$. Теперь посмотрим на все вершины, из которых есть переход в $A$. Тогда эти вершины ведут строки $s[0:k - 1], s[1:k - 1], s[2:k - 1], s[3:k - 1], \ldots, s[l:k - 1]$, и только они. И замечаем, что тогда между этими вершинами как-то расставлены суффиксные ссылки, причём если от предка $A$ спускаться по суффиксным ссылкам, то мы будем идти по вершинам, из которых есть переход в $A$ пока не попадём в какую-то вершину, из которой в $A$ перехода нет. При этом мы пройдём по всем вершинам, из которых есть переход в $A$ и в конце мы окажемся в вершине, которой соответствует строка $s[l + 1:k - 1]$. Заметем, что тогда из этой вершины будет идти переход суффиксную ссылку вершины $A$, и эта вершина как раз будет предком суффиксной ссылки $A$.
И наконец заметим последнюю вещь. Если из вершины есть переход по какому-то символу $c$, то есть вершина, в которую ведёт строка $s + c$, а значит в исходной строке был какой-то суффикс, начинающийся с $s + c$. Тогда у этой же строки есть суффикс, начинающийся с $s[l + 1:k] + c$. Тогда из суффиксной ссылки вершины $A$ тоже должен быть переход по символу $c$. Тогда посмотрим, куда ведут эти 2 перехода. Они могут вести в одну и ту же вершину, а могут вести в разные. Если они ведут в разные, то в первую точно ведёт строка $s[l:k] + c$ (самая минимальная строка, ведущая в $A$ с приписанным к ней символом $c$), а во вторую ведёт строка $s[l + 1:k] + c$ (строка, соответствующая суффиксной ссылке из $A$, с приписанным к ней символом $c$). Замечаем, что это последовательные суффиксы друг друга, значит из первой вершины должна вести суффиксная ссылка во вторую.
Алгоритм
Мы разобрались со всеми определениями, и теперь пора перейти к алгоритму. Алгоритм гораздо легче всей теории, за ним стоящей.
Будем строить суффавтомат итеративно, т.е будем достраивать суффавтомат при приписывании к исходной строке нового символа.
Посмотрим на вершину $A$, которой соответствует вся строка. Как мы знаем, в неё ведёт несколько последовательных суффиксов строки, а следующие суффиксы ведут в её суффиксную ссылку. Если спускаться от этой вершины по суффиксным ссылкам, то мы посетим все терминальные вершины суфф. автомата и только их.
Пусть мы дописали к автомату символ $ch$. Тогда нам надо, чтобы автомат принимал любой суффикс исходной строки с приписанным к нему символом $ch$. Тогда как-то менять нам надо только терминальные вершины, и то не все, ведь из некоторых уже мог быть переход по $ch$.
Делать мы это будем так: создадим вершину $B$ и проведём в неё переход по символу $ch$ из $A$. Далее перейдём в суффиксную ссылку из $A$. Назовём теперь эту вершину именем $A$. Если из нового $A$ нет перехода по символу $ch$, то проведём его тоже в вершину $B$. Далее снова перейдём в суфф. ссылку из $A$, и снова назовём теперь эту вершину именем $A$. Будем продолжать так делать пока из $A$ не появится переход по символу $ch$. Пусть этот переход ведёт в вершину $C$. У нас возможно 2 варианта: $A$ — предок $C$ или $A$ — не предок вершины $C$.
В первом случае всё просто. Проведём суфф ссылку из $B$ в $C$. Замечаем, что после этого для всех старых вершин свойства суффавтомата выполнены, в $B$ будут вести последовательные суффиксы исходной строки с приписанным символом $ch$, и из $B$ будет существовать корректная суффиксная ссылка. Тогда если в новом суффавтомате пометить терминальными все вершины, которые мы посетим спуском из $B$ по суфф. ссылкам, то автомат будет корректным и будет принимать только суффиксы начальной строки с приписаным символом $ch$.
Во втором случае всё тоже просто, но не совсем. Из вершины $B$ мы не можем пустить суфф. ссылку в вершину $C$, потому что в $C$ ведут некоторые строки, не являющиеся суффиксами $B$. Но замечаем, что строка, которая соответствует $A$ с приписанным к ней символом $ch$ ведёт в $C$ и является самым большим суффиксом $B$, не ведущим в $B$. Тогда сделаем следующую вещь. Возьмём вершину $C$ и раздвоим её. Вернее отделим от неё кусок. Возьмём строку, соответствующую $A$, припишем к ней $ch$ и возьмём все её суффиксы, лежащие в $C$. И создадим вершину $D$, в которую будут вести только эти строки. Чтобы эти строки вели в $D$, надо провести туда переходы. Замечаем, что строка, соответствующая $A$ с приписанным $ch$ будет соответствовать $D$, а значит $A$ будет являться предком $D$. Дальше будем спускаться по суффиксным ссылкам из $A$, и пока переход по символу $ch$ будет вести в $C$, будем менять его на $D$, а если переход будет вести куда-то в другое место, то это будет означать, что мы пройдём все вершины, которым соответствуют суффиксы $A$ и из которых переход по $ch$ раньше вёл в $C$. После этого переходы в $D$ будут корректно построены. После этого построим корректно суффиксные ссылки. Проведём из $C$ суффиксную ссылку в $D$ и проведём из $D$ суффиксную ссылку туда, куда она раньше вела из $C$. Так как вершина $D$ является отделённым куском вершина $C$, то все переходы из $D$ будут такими-же, как все переходы из $C$. Тогда замечаем, что после такого разделения вершины $C$ на 2 части автомат всё ещё корректный и его правила выполняются. А так же замечаем, что теперь из $A$ переход по $ch$ ведёт в $D$, и $A$ — предок $D$. Тогда мы свели этот случай к предыдущему и теперь нам достаточно построить переход из $B$ в $D$, и суффавтомат построен. Разумеется, вершины надо помечать терминальными не после каждого добавления символа, а только в самом конце.
Утверждение: (Время работы)
Время построения суффиксного автомата составляет $O(N)$.
Доказательство:
Во первых мы каждый раз создавали не более 2 вершин, т.е. всего вершин $O(n)$. Мы много раз спускались по суффиксным ссылкам из $A$, назовём балансом вершины длину пути от неё до корня по суфф. ссылкам. Тогда баланс $B$ в первом случае это баланс $C$ плюс 1. А баланс $C$ не превышает баланс конечного $A$ плюс 1, т.к. предки вершин на пути от $C$ до корня различны и лежат на пути от конечного $A$ до корня. Тогда если баланс $B$ равен балансу $A$ плюс 1 минус число спусков по $A$. Тогда как было с Ахо-карасиком, число спусков не превышает $n$. Про то, что раздвоение быстро работает можно тоже доказать, но мне лень это писать, так что подумайте сами. В общем там всё работает быстро и общее построение работает за $O(N)$.
Пример реализации
Звучит это всё страшно, но пишется в 40 строк, вот реализация на питоне с кучей ошибок, чтобы вы не копипастили.
1 # Здесь много ошибок, код нужен только для ознакомления
2
3 class node:
4 def init(self):
5 self.nx = [-1] * 26 # Переходы
6 self.p = -1 # Суффиксная ссылка
7 self.pre = -1 # Предок
8
9 s = [node()]
10
11 # Мы по умолчанию считаем, что суффиксная ссылка из корня ведёт в -1
12
13 def add(a, ch): # a - последняя вершина в автомате, ch - добавляемый символ
14 # Создаём вершину b и указываем её правильные параметры
15 b = len(s)
16 s.append(node())
17 s[b].p = 0 # Обратите внимание на это, возможно мы так и не дойдём до вершины С
18 # и тогда суффиксная ссылка из b должна указывать на 0
19 s[b].pre = -1
20 while a != -1:
21 if (s[a].nx[ch] == -1):
22 # Случай, когда из а нет перехода по ch
23 s[b].nx[ch] = a
24 a = s[a].p
25 continue
26 # c - то, куда ведёт переход из a по ch
27 c = s[a].nx[ch]
28 # Проверяем, что предок c это a и в этом случае меняем суфф. ссылку b
29 if (s[c].pre == a):
30 s[b].p = a
31 break
32 # Иначе создаём вершину d
33 d = len(s)
34 s.append(node())
35 # Меняем суфф. ссылки
36 s[c].p = d
37 s[b].p = d
38 s[d].p = s[c].p
39 # Назначаем предка d
40 s[d].pre = b
41 # Копируем переходы
42 s[d].nx = s[c].nx
43 # Добавляем предков вершины d, пройдясь вниз по суфф. ссылкам из a
44 while (a != -1 and s[a].nx[ch] == b):
45 s[a].nx[ch] = d
46 a = s[a].pre
47 break
48 # Если строк несколько, то возможно мы не добавили b. Поэтому надо возвращать вот это
49 return s[s[b].pre].nx[ch]
Задачи
Количество различных подстрок
Замечаем, что любая подстрока строки — это начало какого-то суффикса. Тогда в нашем автомате любой путь — это подстрока начальной строки, и для любой подстроки существует путь в автомате по ней. Тогда первый способ найти число подстрок данной строки — посчитать число путей в автомате. Это можно сделать обычным ДФСом, путём подсчёта для каждой вершины числа путей из неё (только надо запоминать уже посещённые вершины, чтобы 2 раза не ходить). Есть второй способ. Каждый путь заканчивается в какой-то вершине. Тогда для каждой вершины можно посчитать число путей, в неё ведущих. Это можно делать как в процессе построения (но не забывать про пересчёт числа путей в раздваиваемые вершины), так и после. Тогда сумма по кол-ву путей, заканчивающихся в каждой вершине автомата это число различных путей в автомате, т.е. число подстрок данной строки. Этот способ так же позволяет найти число подстрок у каждого префикса строки, так как в процессе построения автомата мы поочерёдно строим суффавтомат для каждого префикса нашей строки.
Рефрен
Рефрен это такая подстрока данной нам строки, что произведение её длины на число вхождений в нашу строку максимально. Найти рефрен очень просто. Замечаем, что число вхождений подстроки в строку это число суффиксов строки, что эта подстрока — начало этого суффикса. Тогда число вхождений подстроки в строку это число путей из вершины, соответствующей этой подстроке, в терминальные вершины. Тогда для каждой вершины посчитаем число путей из неё в терминальные вершины (это делается так же, как и подсчёт числа просто путей из вершины), а так же для каждой вершины посчитаем длину строки, которая ей соответствует. Переберём все вершины и найдём ту, у которой произведение длины на число путей до терминальных вершин будет максимально. Строка, соответствующая этой вершине это и есть рефрен.
Суффиксный автомат для нескольких строк
Всё что будет описано дальше вы нигде больше не прочитаете, потому что никто этого не знает.
Пока мы строили суффавтомат для одной строки. Но замечаем, что при добавлении символа мы никак не использовали то, что суффавтомат должен быть конкретно для одной строки. Мы использовали только то, что вершина принимает последовательные суффиксы и то, что существует суффиксная ссылка. В частности это означало, что если в суффавтомате есть путь, соответствующий какой-то строке, то есть путь, соответствующий любому суффиксу данной строки, а значит и вообще любой подстроке данной строки. Тогда заметим, что мы можем просто взять любую вершину, и дописать к ней переход по какому-то символу, используя наш алгоритм. И никаких проблем от этого не будет. Тогда перейдём к следующей задаче.
Подавтомат
Рассмотрим следующую задачу. Дан набор из $n$ строк, с суммарной длиной $m$. Для каждого $1 \le k \le n$ найти максимальную длину строки, являющейся подстрокой хотя-бы $k$ строк из набора.
Для начала построим суффавтомат, который принимает все суффиксы всех строк из набора. Это делается так: сначала построим автомат для первой строки. Дальше пользуясь важным замечанием возьмём корень автомата, и припишем к нему первый символ второй строки. К этой вершине припишем второй символ второй строки и т. д. (Обратите внимание, что функцию $add$ надо вызывать даже если переход по символу уже был, так как возможно нам придётся раздваивать следующую вершину. Именно поэтому в функции $add$ из примера такой странный return, ведь возможно мы не добавляли перехода в вершину $b$). Так мы получим автомат, принимающий все суффиксы первых двух строк. Дальше так же туда припишем третью, четвёртую и т.д. строки. По сути у нас автомат превратился в бор с уже готовыми суфф. ссылками и принимающий не только строки, но и все их подстроки.
Вы наверное думаете, что всякие-там термины уже закончились. А вот нет.
Определение:
Подавтомат вершины $A$ —это такая часть вершин нашего автомата, что в ней есть пути по всем подстрокам строки, соответствующей вершине $A$, и только по ним.
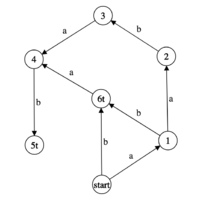
Если рассмотреть уже встречавшийся ранее пример суфф. автомата для строки «aabab», то в подавтомат вершины 3 войдут вершины $start, 1, 2, 3, 6t$, в подавтомат вершины $6t$ войдут вершины $start, 1, 6t$, а в подавтомат вершины $2$ войдут только вершины $start, 1, 2$.
Заметим, что чтобы построить подватомат вершины $A$, нам достаточно построить подавтомат её предка, а так же добавить туда все вершины, достижимые из $A$ спуском по суфф. ссылкам. (Это верно, так как подавтомат предка принимает подстроки $A$ без последнего символа, а оставшиеся подстроки $A$ это суффиксы $A$, т.е. то, что мы пройдём, когда будем спускаться по суфф. ссылкам. Заметим, что тогда мы можем сказать, что подавтомат вершины $A$ это сама вершина $A$ и объединение подавтоматов её суфф. ссылки и её предка. А тогда с помощью очень простой рекурсивной функции $subautomaton$ мы можем пройти по всем вершинам подавтомата.
1 class node:
2 def init(self):
3 self.nx = [-1] * 26 # Переходы
4 self.p = -1 # Суффиксная ссылка
5 self.pre = -1 # Предок
6 self.last_used = -1 # Время последнего посещения
7
8 s = [node()] # Список вершин
9
10 t = 0 # Временная метка построения подавтомата
11 # (нужно чтобы не посещать одну и ту же вершину несколько раз)
12
13 # Делает какое-то действие для подавтомата вершины
14 # При каждом следующем запуске временную метку t надо менять
15 def subautomaton(a):
16 # Проверка, что при этом построении подавтомата мы ещё не посещали вершину
17 if (s[a].last_used == t):
18 return
19 s[a].last_used = t
20 # Делаем какое-то действие
21 subautomaton(s[a].p) # Идём в суфф. ссылку
22 subautomaton(s[a].pre) # Идём в предка
Теперь вернёмся к задаче. Попробуем для каждой строки найти число строк из набора, а которых эта строка является подстрокой. Для этого нам надо для каждой вершины узнать, у скольких строк из из набора эта вершина является подстрокой. А для этого нам достаточно посмотреть на каждую вершину, соответствующую какой-то строке из набора. Мы знаем, что все вершины в её подавтомате как раз являются её подстроками. Тогда для каждой вершины заведём счётчик числа строк, в которой она является подавтоматом. И для каждой строки из набора прибавим 1 к счётчикам всех строк в подавтомате. Для каждой вершины так же запомним длину строки, соответствующей этой вершине. И дальше просто переберём все вершины и обновим через них ответ.
Остаётся один непонятный вопрос — время работы нашего алгоритма. Это только в обычном суффавтомате число вершин $O(n)$. Но тут берётся подавтомат, и вообще может оказаться, что каждой подстроке подавтомата соответствует по отдельной вершине, и тогда у нас будет $l^2$ вершин в подавтомате, где $l$ — длина строки, для которой мы строим подавтомат. Что-же, получается наш алгоритм работает за $O(n \cdot m^2)$. А вот нифига подобного. У нас всего вершин в автомате будет $O(m)$, значит число вершин в податомате не больше $O(m)$. Но асимптотика $O(n \cdot m)$ нас тоже не очень-то устраивает. Тогда разделим все строки из набра на короткие и длинные. В коротких число символов должно быть не больше $\sqrt{m}$, а в длинных может быть больше. Заметим, что число длинных строк не больше $\sqrt{m}$, значит величина всех их подавтоматов $O(m \cdot \sqrt{m})$. А что делать с короткими строками. Как мы знаем, для строки $l$, размер её подавтомата не больше $l^2$. А это меньше, чем $l \cdot \sqrt{m}$. Тогда суммарный размер подавтоматов коротких строк это $\sum l \cdot \sqrt{m} = \sqrt{m} \cdot \sum l$. А сумма длин всех строк не больше $m$. Тогда суммарный размер всех подавтоматов $O(m \sqrt{m})$. Но так как про эту идею никто не знает, никто не строит антитесты, на которых это работает за $O(m \sqrt{m})$. Поэтому этот алгоритм просто летает и спокойно заходит даже при $m = 5\,000\,000$. И вот это вот позволяет вам становиться богом строк и решать почти любую задачу на одну или несколько строк. Скажем вот:
Ахо-карасик в онлайне с линейной памятью
Есть 3 онлайн запроса: добавить в набор строку, удалить из набора строку и для данной строки узнать суммарное число вхождений строк из набора в качестве подстроки.
Запросы первого и второго вида будем обрабатывать очень просто. Если пришла новая строка, то добавим её в автомат и пометим её последнюю вершину терминальной. Если пришёл запрос удаления, то уберём терминальную пометку.
На запрос третьего типа будем отвечать так: добавим строку в автомат, пройдёмся по вершинам, отвечающим за префиксы этой строки. И будем спускаться из них по суфф. ссылкам и если прошли через терминальную вершину, то прибавлять 1 к ответу. Логично, что это будет долго работать. Но сделаем так: если мы оказались в какой-то вершине, через которую уже так вот спускались по суфф. ссылкам, то не будем идти так же ещё раз, а просто прибавим заранее посчитанный ответ для неё. Тогда по каждой вершине подавтомата данной строки мы пройдёмся по разу. А значит время работы будет $O(m \cdot \sqrt{m})$.
Завершение
Суфф. автоматом можно решать много других задач. Код суфф. автомата очень простой, и часто для построения даже обычного ахо карасика можно его заюзать. Так же если вдруг вам припрёт написать задачу не суфф. автоматом, а суфф. деревом или суфф. массом, то сообщаем, что Укконен — это явно не то, чем стоит строить суфф. дерево (а из него уже суфф. масс). Просто постройте суфф. автомат для перевёрнутой строки, возьмите дерево суффиксных ссылок, это и будет суфф. дерево для начальной строки. Доказательство этого факта оставим читателю в качестве упражнения.
И ещё раз напомню, что для дебага суфф. автомата надо использовать строку «aabab». Если суфф. автомат на ней правильно построен, то с вероятностью $99\%$ ваш код правильный.
Упражнения
Попробуйте решить сформулированную выше задачу про длину максимальной подстроки у $k$ строк для каждого $k$, суммарно за линейное время.
Автор конспекта: Филипп Грибов
По всем вопросам пишите в telegram @grphil