Поиск мостов: различия между версиями
Debnatkh (обсуждение | вклад) (Новая страница: «Пусть дан связный неориентированный граф. Мост - ребро, при удалении которой граф станов...») |
м |
||
| (не показаны 4 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | '''Определение.''' ''Мостом'' называется ребро, при удалении которого связный неориентированный граф становится несвязным. | |
| − | + | Пример задачи, где их интересно искать: дана топология сети (компьютеры и физические соединения между ними) и требуется установить все единые точки отказа — узлы и связи, без которых будут существовать два узла, между которыми не будет пути. | |
| − | + | Наивный алгоритм поочередного удаления каждого ребра <math>(u, v)</math> и проверки наличия пути <math>u \leadsto v</math> потребует <math>O(m^2)</math> операций. Чтобы научиться находить мосты быстрее, сначала сформулируем несколько утверждений, связанных с обходом в глубину. | |
| − | + | Запустим DFS из произвольной вершины. Введем новые виды рёбер: | |
| − | + | * ''Прямые'' рёбра — те, по которым были переходы в dfs. | |
| − | + | * ''Обратные'' рёбра — то, по которым не было переходов в dfs. | |
| − | |||
| − | |||
| − | , в | ||
| − | |||
| − | |||
| − | + | Заметим, что никакое обратное ребро <math>(u, v)</math> не может являться мостом: если его удалить, то всё равно будет существовать какой-то путь от <math>u</math> до <math>v</math>, потому что подграф из прямых рёбер является связным деревом. | |
| − | |||
| − | |||
| − | u | ||
| − | , | ||
| − | + | Значит, остается только проверить все прямые рёбра. Это уже немного лучше — такой алгоритм будет работать за <math>O(n m)</math>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Сооптимизировать его до линейного времени (до одного прохода dfs) поможет замечание о том, что обратные рёбра могут вести только «вверх» — к какому-то предку в дереве обхода графа, но не в другие «ветки» — иначе бы dfs увидел это ребро раньше, и оно было бы прямым, а не обратным. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ( | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | , | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[File:Http---codeforces.com-predownloaded-e4-11-e4112103b65ad2cb3287cf9df022ac858ff15554.png|frame|none]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | - | ||
| − | + | Тогда, чтобы определить, является ли прямое ребро <math>v \to u</math> мостом, мы можем воспользоваться следующим критерием: глубина <math>h_v</math> вершины <math>v</math> меньше, чем минимальная глубина всех вершин, соединенных обратным ребром с какой-либо вершиной из поддерева <math>u</math>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | , | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | , | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Для ясности, обозначим эту величину как <math>d_u</math>, которую можно считать во время обхода по следующей формуле: | |
| + | |||
| + | <math> | ||
| + | d_v = \min \begin{cases} | ||
| + | h_v, &\\ | ||
| + | d_u, &\text{ребро } (v \to u) \text{ прямое} \\ | ||
| + | h_u, &\text{ребро } (v \to u) \text{ обратное} | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | Если это условие (<math>h_v < d_u</math>) не выполняется, то существует какой-то путь из <math>u</math> в какого-то предка <math>v</math> или саму <math>v</math>, не использующий ребро <math>(v, u)</math>, а в противном случае — наоборот. | ||
| + | |||
| + | <source lang="cpp">const int maxn = 1e5; | ||
| + | |||
| + | bool used[maxn]; | ||
| + | int h[maxn], d[maxn]; | ||
| + | |||
| + | void dfs(int v, int p = -1) { | ||
| + | used[u] = true; | ||
| + | d[v] = h[v] = (p == -1 ? 0 : h[p] + 1); | ||
| + | for (int u : g[v]) { | ||
| + | if (u != p) { | ||
| + | if (used[u]) // если ребро обратное | ||
| + | d[v] = min(d[v], h[u]); | ||
| + | else { // если ребро прямое | ||
| + | dfs(u, v); | ||
| + | d[v] = min(d[v], d[u]); | ||
| + | if (h[v] < d[u]) { | ||
| + | // ребро (v, u) -- мост | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | }</source> | ||
| + | '''Примечание.''' Более известен алгоритм, вместо глубин вершин использующий их <math>tin</math>, но автор считает его чуть более сложным для понимания. | ||
Текущая версия на 13:56, 2 июля 2021
Определение. Мостом называется ребро, при удалении которого связный неориентированный граф становится несвязным.
Пример задачи, где их интересно искать: дана топология сети (компьютеры и физические соединения между ними) и требуется установить все единые точки отказа — узлы и связи, без которых будут существовать два узла, между которыми не будет пути.
Наивный алгоритм поочередного удаления каждого ребра \((u, v)\) и проверки наличия пути \(u \leadsto v\) потребует \(O(m^2)\) операций. Чтобы научиться находить мосты быстрее, сначала сформулируем несколько утверждений, связанных с обходом в глубину.
Запустим DFS из произвольной вершины. Введем новые виды рёбер:
- Прямые рёбра — те, по которым были переходы в dfs.
- Обратные рёбра — то, по которым не было переходов в dfs.
Заметим, что никакое обратное ребро \((u, v)\) не может являться мостом: если его удалить, то всё равно будет существовать какой-то путь от \(u\) до \(v\), потому что подграф из прямых рёбер является связным деревом.
Значит, остается только проверить все прямые рёбра. Это уже немного лучше — такой алгоритм будет работать за \(O(n m)\).
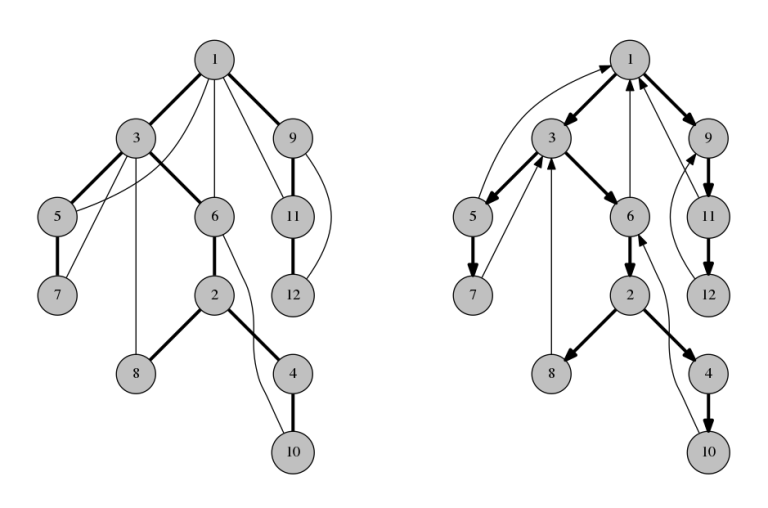
Сооптимизировать его до линейного времени (до одного прохода dfs) поможет замечание о том, что обратные рёбра могут вести только «вверх» — к какому-то предку в дереве обхода графа, но не в другие «ветки» — иначе бы dfs увидел это ребро раньше, и оно было бы прямым, а не обратным.
Тогда, чтобы определить, является ли прямое ребро \(v \to u\) мостом, мы можем воспользоваться следующим критерием: глубина \(h_v\) вершины \(v\) меньше, чем минимальная глубина всех вершин, соединенных обратным ребром с какой-либо вершиной из поддерева \(u\).
Для ясности, обозначим эту величину как \(d_u\), которую можно считать во время обхода по следующей формуле\[ d_v = \min \begin{cases} h_v, &\\ d_u, &\text{ребро } (v \to u) \text{ прямое} \\ h_u, &\text{ребро } (v \to u) \text{ обратное} \end{cases} \]
Если это условие (\(h_v < d_u\)) не выполняется, то существует какой-то путь из \(u\) в какого-то предка \(v\) или саму \(v\), не использующий ребро \((v, u)\), а в противном случае — наоборот.
const int maxn = 1e5;
bool used[maxn];
int h[maxn], d[maxn];
void dfs(int v, int p = -1) {
used[u] = true;
d[v] = h[v] = (p == -1 ? 0 : h[p] + 1);
for (int u : g[v]) {
if (u != p) {
if (used[u]) // если ребро обратное
d[v] = min(d[v], h[u]);
else { // если ребро прямое
dfs(u, v);
d[v] = min(d[v], d[u]);
if (h[v] < d[u]) {
// ребро (v, u) -- мост
}
}
}
}
}
Примечание. Более известен алгоритм, вместо глубин вершин использующий их \(tin\), но автор считает его чуть более сложным для понимания.